Money-Weighted Rate of Return – Loan and Investment Programs Selection

435

The Money-Weighted Rate of Return (MWRR) calculates the periodic rate of return that makes the present value of cash inflows and outflows zero. It can be seen as the average rate of return for the period and is defined as the Internal Rate of Return (IRR).

The MWRR is influenced by investment and withdrawal amounts, making it unsuitable as an evaluation tool for investment performance but an optimal tool for different plan selections.

In making financial decisions, individuals typically fall into two categories: loan decisions or investment decisions. Loan decisions involve initially lending money to you (cash inflow), with subsequent repayments at different time points (cash outflow). Investment decisions entail initially investing money in a particular asset (cash outflow), followed by returns at different time points (cash inflow).

Whether it’s a loan or an investment, the only difference lies in the timing of cash inflows and outflows. The MWRR can be calculated for all these cash flows.

If it’s a loan decision, the MWRR represents your cost of funds. Opt for the loan scheme with the lowest MWRR.

If it’s an investment decision, the Money-Weighted Rate of Return represents your investment return. Choose the investment scheme with the highest MWRR.

To focus on the application of this MWRR, let’s use a practical example. We will only consider confirmed amounts and periods in the scenarios, excluding factors such as uncertain amounts, periods, and risk costs.

Calculations for the following scenarios can be done using a spreadsheet. Set cash inflows as positive values (representing received funds) and cash outflows as negative values (representing expended funds). Utilize the IRR function to determine the MWRR.

Spreadsheet calculation of the MWRR for cash flows

A certain plan involves receiving funds (cash inflow) of 200,000 in the first month, followed by cash outflows of 30,000, 20,000, 10,000, 150,000, and 20,000 in the second to sixth months, respectively.

In the same row of the spreadsheet, input cash flows according to the order of periods. Enter positive values for cash inflows and negative values for cash outflows.

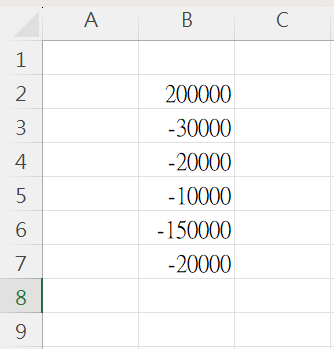
Calculate the MWRR

Utilizing the IRR function in the spreadsheet, selecting the entire cash flow for the period, the calculated MWRR (IRR) is 4.13%

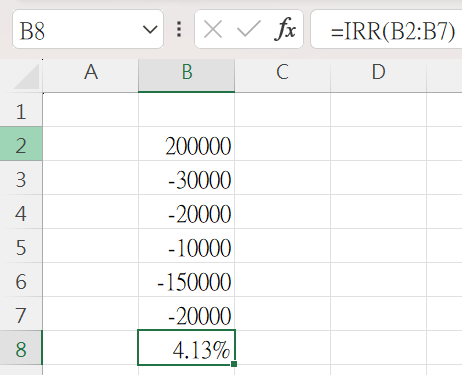
The Meaning of the MWRR

If the rate of return for each period is 4.13%, it can make the overall cash flow reach zero at the end of the period. This means that if you borrow 200,000 for investment, the average rate of return per period needs to be higher than 4.13% to repay future cash outflows, ensuring that the ending balance is above zero (making a profit from the investment).

• Current investment profit = (Initial assets – Repayment amount) * 4.13%
• End assets = Begin assets – Repayment amount + Investment profit

Comparison of loan and investment programs – Application of MWRR

Which bank’s loan program should I choose?

Banks will inform you of the loan interest rates and provide various repayment options, such as processing fees, equal principal and interest amortization, grace periods, etc. You may find it challenging to decide due to the multitude of choices offered by the banks.

We can calculate the MWRR for these loan programs to choose the one with the lowest cost of capital.

Confirm the amounts and timing of cash inflows and outflows, and request the bank to provide relevant data such as the monthly repayment amount and processing fees for the loan amount.

Input the cash flows for each period, including borrowing, repayment, processing fees, etc., into the sheets

• Borrowing amount represents cash inflow, input as a positive value for that period.
• Repayment amount represents cash outflow, input as a negative value for that period.
• Processing fees represent an initial cash outflow, input as a negative value for that period.

Apply the sheets to calculate the MWRR for the loan program

The MWRR for the loan program, which represents the cost of borrowing funds, is equivalent to the monthly interest rate when the periods are measured in months.

Compare the costs of various loan programs and choose the one with the lowest MWRR

I have many loans; should I choose from various alternative repayment plans offered by the bank?

The repayment plan refers to transferring multiple existing loans to another bank or lending institution, using a new loan to pay off the existing ones. This method is often referred to as debt consolidation or loan transfer.

The purpose of debt consolidation is to convert high-interest loans into lower-interest ones, reducing your interest burden and monthly payment amounts. This can help you manage debt more effectively, alleviate financial pressure, and save on interest expenses. However, choosing a repayment plan often involves additional costs such as processing fees, credit inquiry fees, early repayment fees, etc. To determine whether using a repayment plan is cost-effective, we can use the MWRR to evaluate whether adopting the repayment plan is a suitable approach for managing existing multiple loans. The calculation assumes that the loan amount from the repayment plan can fully repay all existing loans.

It is essential to confirm the outstanding balances of existing loans, future repayment amounts for each period, the loan amount and repayment schedule for the repayment plan, as well as associated fees such as processing fees and credit inquiry fees.

Calculate the average cost of capital for the current loan amount(MWRR)

• Sum the repayment amounts for each period for multiple existing loans as the cash outflows.
• Sum the outstanding balances of multiple existing loans and input them into the financial statement as the cash inflow for the first period.
• Apply the IRR function of the sheets to calculate the average cost of capital for multiple loans – the MWRR.

Calculate the average cost of capital for the repayment plan(MWRR)

• The loan amount of the repayment plan is the initial cash inflow.
• The processing fees, credit inquiry fees, and prepayment fees for existing loans in the repayment plan are the initial cash outflow.
• The repayment amounts of the repayment plan are the cash outflows for each period.
• Apply the IRR function of the financial statement to calculate the average cost of capital for the repayment plan – the MWRR.

比Compare the average cost for the current loans with the average cost of capital for the repayment plan and choose the plan with the lower MWRR.

Choosing Between Fixed-Term Deposits and Short-Term Savings Insurance

Banks offer a wide range of investment options, and for conservative investors, the main choices often boil down to fixed-term deposits and short-term savings insurance. Disregarding factors like insurance risk costs and liquidity costs, the decision between these two options can be made by calculating the amount-weighted rate of return (MWRR).

Short-term savings insurance’s predetermined interest rate doesn’t directly represent your return. Calculating the MWRR for both options allows for a more accurate comparison.

Confirm the deposit amount, end-of-term payment amount for fixed-term deposit, premium for short-term life insurance, and the repayment amount at maturity.

Calculate the MWRR for the fixed-term deposit

• The initial deposit amount for a fixed-term deposit is considered as the cash outflow for the first period.
• If the fixed-term deposit matures after one year, the cash inflow for the second period is the receipt amount.
• If the deposit is renewed upon maturity, you can follow the above explanation to set the cash flows for each period.
• Use the IRR function in the spreadsheet to calculate the Money-Weighted Rate of Return (MWRR) for the fixed-term deposit amount.

Calculate the Money-Weighted Rate of Return (MWRR) for short-term savings insurance.

• The annual premium for short-term savings insurance is considered as the cash outflow. Set the cash outflow for each period based on the respective annual premium amounts.
• The return amount for short-term savings insurance is considered as the cash inflow. Set the cash inflow for each period based on the respective return amounts.
• Use the IRR function in the spreadsheet to calculate the Money-Weighted Rate of Return (MWRR) for short-term savings insurance.

Compare the investment returns of fixed-term deposits and short-term savings insurance, and choose the investment plan with a higher MWRR

Money-Weighted Rate of Return for Financial Goals

Financial goals refer to specific objectives or sets of objectives that individuals or families pursue in financial management. Financial goals can vary from person to person and are determined by individual values, life stages, and financial needs. Examples of financial goals include an emergency fund, retirement plan, children’s education fund, homeownership plan, debt management, and goals related to a comfortable lifestyle.

To achieve financial goals, individuals often use various sources of income such as salaries, sales, and retirement funds. After deducting daily living expenses, they allocate funds to savings or investments to meet the needs of their financial goals.

When setting financial goals, there are often the following uncertainties:

• Can these incomes support the expenses for my financial goals?
• If not, do I need to make high-risk investments to meet the expenses?
• Or should I consider lowering my financial goals?

We can apply the MWRR to address these questions.

Confirming current income, anticipated future income, existing expenses, future monthly amounts for financial goals, and considering inflation.

Setting the amounts for income and expenses in each period on the spreadsheet.

• Income is considered as cash inflow.
• Expenses are considered as cash outflow.
• Summing up the cash inflows and outflows for each period.

Applying the IRR function in a spreadsheet to calculate the MWRR for financial goals

Money-Weighted Rate of Return for Financial Goals: The minimum rate of return that needs to be achieved when saving or investing current and future income to meet the financial goals.

結論

金額加權報酬率（Money-Weighted Rate of Return）是一種衡量借款成本或投資報酬率的指標，基於以上對金額加權報酬率的討論，以下表來總結分析：

Calculating the Money-Weighted Rate of Return can be challenging, especially when inputting the spreadsheet, as it requires summing up cash inflows and outflows for each period. Additionally, financial goals need to consider factors such as inflation, salary increase rates, and when there are multiple financial goals, it becomes even more complex.

Vision Money can directly set financial goals and automatically calculate the cash flows for each period considering the impact of inflation, significantly reducing the complexity of cash flow settings. This allows you to focus on important decisions such as plan selection and financial goal formulation.

Reference to: Vision Money: Financial Goal Examples